[WIP] Elo Loss: From Chess Ratings to Objective Functions

Preface

I rewatched the DeepMind documentary on AlphaGo recently on whim. They mentioned the Elo Rating used to rate players in competitive games like Chess, Go, Baseball, general boardgames, and more. This suddenly got me curious about the scoring system and I read up quite a bit about it.

In this post, I document my rather crazy idea of repurposing the Elo Rating formula into a loss function to train networks and somehow, it worked out pretty well. I describe my experimental setup and showcase some interesting results.

Elo Rating

Elo rating is used to calculate relative skills levels between players. Players in such games all start off with a base rating and move up the ladder based on calculations involving the Elo rating. It looks rather convoluted and a quick internet search doesn’t give much information on it either. Let me quickly break it down for you here. For starters, given two players A and B, the formula looks like this:

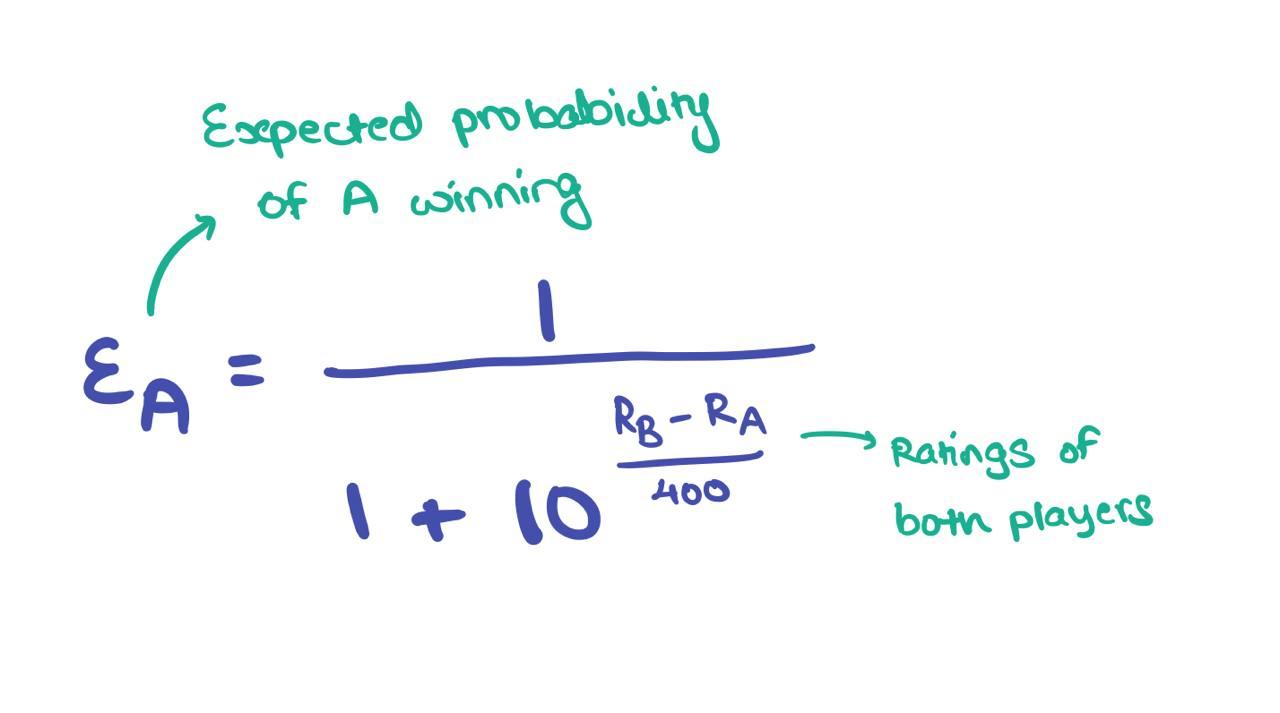
\(E_A\) denotes the expected probability of A winning the game giving \(R_A\) and \(R_B\), the ratings of players A and B respectively; ultimately, we’re calculating \(P(\text{A wins})\). You can do this for player B too: in the denominator, you have to switch it to \(R_A - R_B\) instead. This function always gives a probability value \(\leq 1\).

To update the score for player X, the following formula is used:

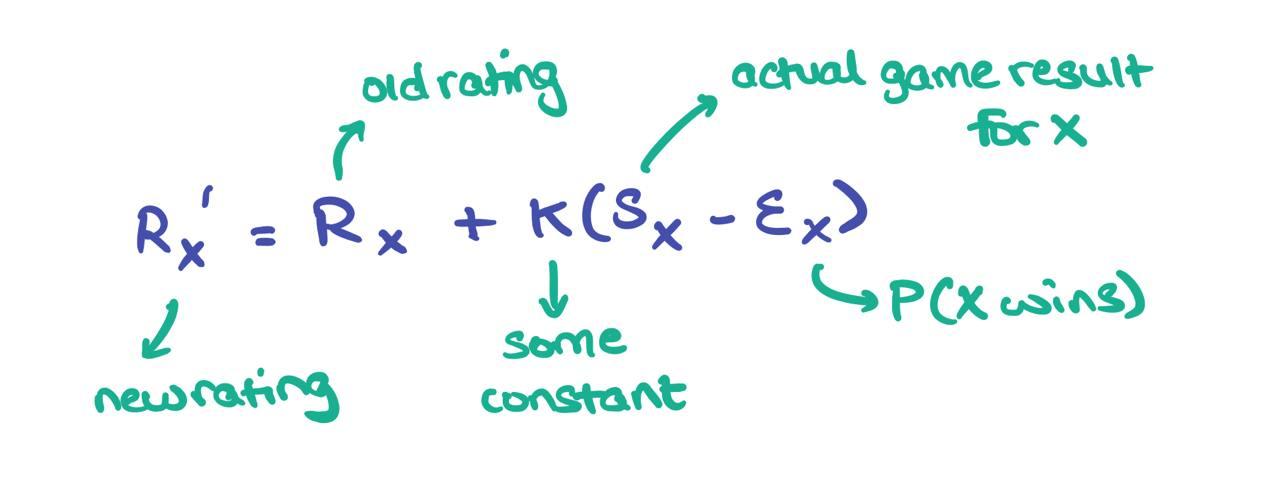
where \(K\) is some constant usually set by tournament’s presiding members and \(S_X=\{1, 0, \frac{1}{2}\}\) is the result of the game (\(1\) means win, \(0\) means lose, \(\frac{1}{2}\) is draw). In fact, if you realise, the lower the expected score \(E_X\), the higher the “surprise” of player X winning the game (i.e., \(S_X=1\)), resulting in a proportionally higher score hike for X. Likewise, if it’s rather “duh” the player X will highly likely win (i.e., a high #\(E_X\)), the lower the score hike for them.

Of course, this update step is not of concern in this blog post. It’s just a funky detail I decided to add for brevity.

Using Elo as a loss function

The Elo score function \(E_X\) for some player X is an example of a logistic function that has the following general form:

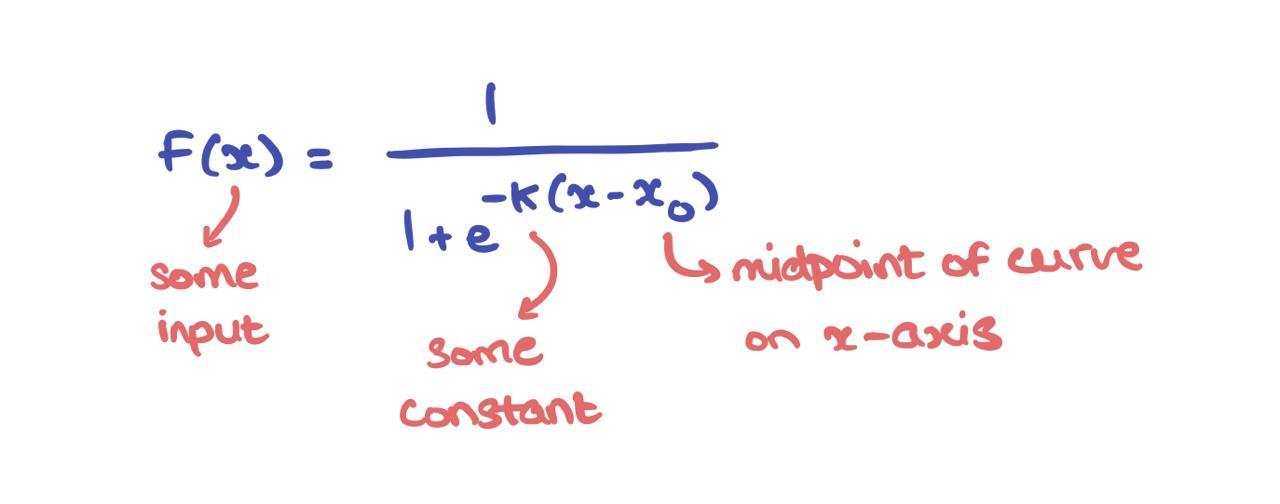
In fact, when \(L=1\), \(k=1\), and \(x_0 = 1\), it’s called a Sigmoid i.e., the activation function used to inject non-linearity into perceptrons and neural networks; it’s mainly used in binary classification problems given some classification threshold. Here, however, I use this Elo logistic function as a loss function, not an activation. It’s best to make that distinction before showcasing some interesting results.

An interesting project for the future would be to evaluate different logistic losses while playing around with values of \(L\), \(k\), and \(x_0\).

This so-called Elo Loss can be formulated as follows:

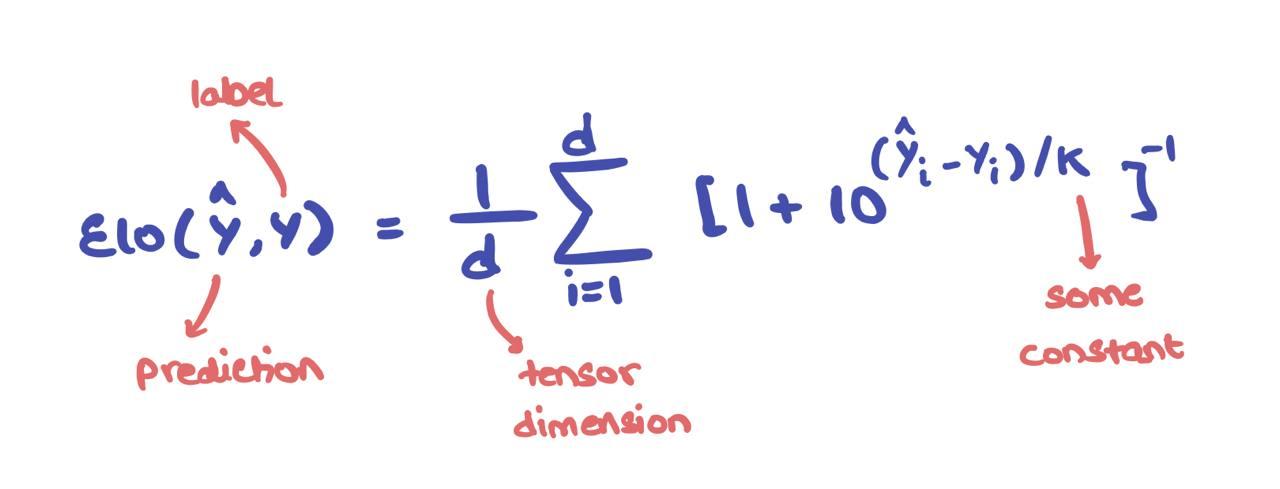
where \(\hat{y}\) is the prediction, \(y\) is the label, and \(m\) is the batch/minibatch size. The \(\hat{y}\) and \(y\) terms \(\in \mathbb{R}^d\) can either be tensors or scalars. This can be considered in the batch/minibatch setting as well by performing this computation over all samples in question.

Results and Discussion

I trained a standard MLP using Elo Loss and standard Cross Entropy Loss on MNIST and CIFAR-10. I repeated the experiments with a CNN using a similar set-up but with the additional Fashion MNIST dataset included. I followed a liberal training regime. For some NLP tasks, I looked at sentiment analysis and trained LSTMs using Cross Entropy and Elo Loss.

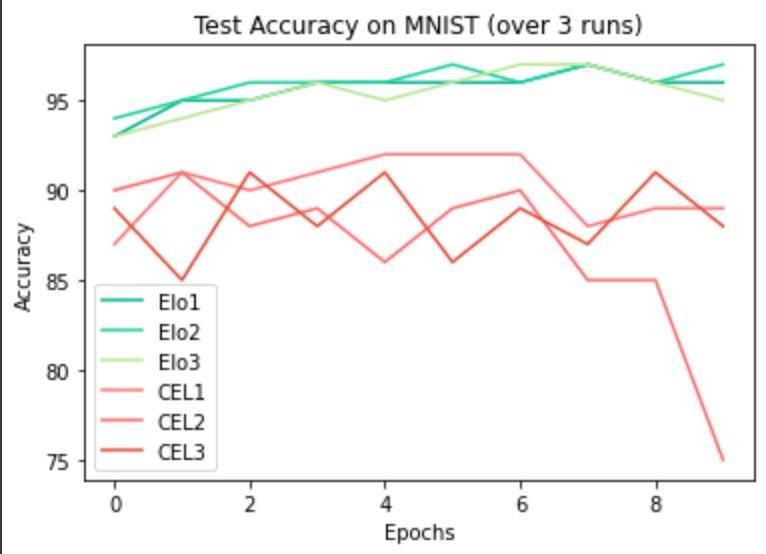
I had a conversation with Lucas Beyer from Google AI a while back (thread). When comparing models across \(N\) runs, do not average the accuracies or seed the models. While the intention to maintain fairness is valid, there are better ways of going about it. For that very purpose, I’ve included multiple plots on the same graph to show some “in the wild” performance. Other than loss, I’ve kept the model architecture, optimiser, and miscellaneous hyper-parameters (learning rate, momentum, etc.) constant for all runs. I’ve been told this is a better way of reporting “fair” results.

MLP on MNIST

CNN on CIFAR-10

CNN on Fashion MNIST

LSTM on Sentiment Analysis

Actor-Critic on ATARI

Here, I picked 3 games: Breakout-v0, Pong-v0, and CartPole-v1.

Final Remarks

Here, I use the Elo rating system as a loss function. I’m not entirely sure if this has been done before based on a quick search online. I’m guessing any decent differentiable function can be used as a loss. This gets me thinking about the desirable characteristics of loss functions in general, aside from differentiability.